Chapter III

Emitted Energy. Stationary State

150. Whereas the absorption of radiation by an oscillator takes place in a perfectly continuous way, so that the energy of the oscillator increases continuously and at a constant rate, for its emission we have, in accordance with Sec. 147, the following law: The oscillator emits in irregular intervals, subject to the laws of chance; it emits, however, only at a moment when its energy of vibration is just equal to an integral multiple $n$ of the elementary quantum $ε = h ν$ , and then it always emits its whole energy of vibration $n ε$ .

We may represent the whole process by the following figure in which the abscissæ represent the time $t$ and the ordinates the energy

(251)

$U = n ε + ρ, (ρ < ε)$

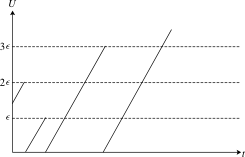
Fig. 7

of a definite oscillator under consideration. The oblique parallel lines indicate the continuous increase of energy at a constant rate

(252)

$\frac{d U}{d t} = \frac{d ρ}{d t} = a,$

which is, according to (249), caused by absorption at a constant rate. Whenever this straight line intersects one of the parallels to the axis of abscissæ $U = ε$ , $U = 2 ε, \dots$ emission may possibly take place, in which case the curve drops down to zero at that point and immediately begins to rise again.

151. Let us now calculate the most important properties of the state of statistical equilibrium thus produced. Of the $N$ oscillators situated in the field of radiation the number of those whose energy at the time $t$ lies in the interval between $U = n ε + ρ$ and $U + d U = n ε + ρ + d ρ$ may be represented by

(253)

$N R_{n, ρ} d ρ,$

where $R$ depends in a definite way on the integer $n$ and the quantity $ρ$ which varies continuously between $0$ and $ε$ .

After a time $d t = \frac{d ρ}{a}$ all the oscillators will have their energy increased by $d ρ$ and hence they will all now lie outside of the energy interval considered. On the other hand, during the same time $d t$ , all oscillators whose energy at the time $t$ was between $n ε + ρ - d ρ$ and $n ε + ρ$ will have entered that interval. The number of all these oscillators is, according to the notation used above,

(254)

$N R_{n, ρ - d ρ} d ρ .$

Hence this expression gives the number of oscillators which are at the time $t + d t$ in the interval considered.

Now, since we assume our system to be in a state of statistical equilibrium, the distribution of energy is independent of the time and hence the expressions (253) and (254) are equal, i.e.,

(255)

$R_{n, ρ - d ρ} = R_{n, ρ} = R_{n} .$

Thus $R_{n}$ does not depend on $ρ$ .

This consideration must, however, be modified for the special case in which $ρ = 0$ . For, in that case, of the oscillators, $N = R_{n - 1} d ρ$ in number, whose energy at the time $t$ was between $n ε$ and $n ε - d ρ$ , during the time $d t = \frac{d ρ}{a}$ some enter into the energy interval (from $U = n ε$ to $U + d U = n ε + d ρ$ ) considered; but all of them do not necessarily enter, for an oscillator may possibly emit all its energy on passing through the value $U = n ε$ . If the probability that emission takes place be denoted by $η$ ( $< 1$ ) the number of oscillators which pass through the critical value without emitting will be

(256)

$N R_{n - 1} (1 - η) d ρ,$

and by equating (256) and (253) it follows that

$R_{n} = R_{n - 1} (1 - η),$

and hence, by successive reduction,

(257)

$R_{n} = R_{0} {(1 - η)}^{n} .$

To calculate $R_{0}$ we repeat the above process for the special case when $n = 0$ and $ρ = 0$ . In this case the energy interval in question extends from $U = 0$ to $d U = d ρ$ . Into this interval enter in the time $d t = \frac{d ρ}{a}$ all the oscillators which perform an emission during this time, namely, those whose energy at the time $t$ was between $ε - d ρ$ and $ε$ , $2 ε - d ρ$ and $2 ε$ , $3 ε - d ρ$ and $3 ε \dots$ . The numbers of these oscillators are respectively

$N R_{0} d ρ, N R_{1} d ρ, N R_{2} d ρ,$

hence their sum multiplied by $η$ gives the desired number of emitting oscillators, namely,

(258)

$N η (R_{0} + R_{1} + R_{2} + \dots) d ρ,$

and this number is equal to that of the oscillators in the energy interval between $0$ and $d ρ$ at the time $t + d t$ , which is $N R_{0} d ρ$ . Hence it follows that

(259)

$R_{0} = η (R_{0} + R_{1} + R_{2} + \dots) .$

Now, according to (253), the whole number of all the oscillators is obtained by integrating with respect to $ρ$ from $0$ to $ε$ , and summing up with respect to $n$ from $0$ to $\infty$ . Thus

(260)

$N = N \sum_{n = 0}^{n = \infty} \int_{0}^{ε} R_{n, ρ} d ρ = N \sum R_{n} ε$

and

(261)

$\sum R_{n} = \frac{1}{ε} .$

Hence we get from (257) and (259)

(262)

$R_{0} = \frac{η}{ε}, R_{n} = \frac{η}{ε} {(1 - η)}^{n} .$

152. The total energy emitted in the time element $d t = \frac{d ρ}{a}$ is found from (258) by considering that every emitting oscillator expends all its energy of vibration and is

$\begin{array}{l} N η d ρ (R_{0} + 2 R_{1} + 3 R_{2} + \dots) ε \\ = & N η d ρ η (1 + 2 (1 - η) + 3 {(1 - η)}^{2} + \dots) \\ = & N d ρ = N a d t . \end{array}$

It is therefore equal to the energy absorbed in the same time by all oscillators (250), as is necessary, since the state is one of statistical equilibrium.

Let us now consider the mean energy $Ū$ of an oscillator. It is evidently given by the following relation, which is derived in the same way as (260):

(263)

$N Ū = N \sum_{0}^{\infty} \int_{0}^{ε} (n ε + ρ) R_{n} d ρ .$

From this it follows by means of (262), that

(264)

$Ū = (\frac{1}{η} - \frac{1}{2}) ε = (\frac{1}{η} - \frac{1}{2}) h ν .$

Since $η < 1$ , $Ū$ lies between $\frac{h ν}{2}$ and $\infty$ . Indeed, it is immediately evident that $Ū$ can never become less than $\frac{h ν}{2}$ since the energy of every oscillator, however small it may be, will assume the value $ε = h ν$ within a time limit, which can be definitely stated.

153. The probability constant $η$ contained in the formulæ for the stationary state is determined by the law of emission enunciated in Sec. 147. According to this, the ratio of the probability that no emission takes place to the probability that emission does take place is proportional to the intensity $I$ of the vibration exciting the oscillator, and hence

(265)

$\frac{1 - η}{η} = p I$

where the constant of proportionality is to be determined in such a way that for very large energies of vibration the familiar formulæ of classical dynamics shall hold.

Now, according to (264), $η$ becomes small for large values of $Ū$ and for this special case the equations (264) and (265) give

$Ū = p h ν I,$

and the energy emitted or absorbed respectively in the time $d t$ by all $N$ oscillators becomes, according to (250),

(266)

$\frac{N I}{4 L} d t = \frac{N Ū}{4 L p h ν} d t .$

On the other hand, H. Hertz has already calculated from Maxwell’s theory the energy emitted by a linear oscillator vibrating periodically. For the energy emitted in the time of one-half of one vibration he gives the expression51

$\frac{π^{4} E^{2} l^{2}}{3 λ^{3}}$

where $λ$ denotes half the wave length, and the product $E l$ (the $C$ of our notation) denotes the amplitude of the moment $f$ (Sec. 135) of the vibrations. This gives for the energy emitted in the time of a whole vibration

$\frac{16 π^{4} C^{2}}{3 λ^{3}}$

where $λ$ denotes the whole wave length, and for the energy emitted by $N$ similar oscillators in the time $d t$

$N \frac{16 π^{4} C^{2} ν^{4}}{3 c^{3}} d t$

since $λ = \frac{c}{ν}$ . On introducing into this expression the energy $U$ of an oscillator from (205), (207), and (208), namely

$U = 2 π^{2} ν^{2} L C^{2},$

we have for the energy emitted by the system of oscillators

(267)

$N \frac{8 π^{2} ν^{2} U}{3 c^{3} L} d t$

and by equating the expressions (266) and (267) we find for the factor of proportionality $p$

(268)

$p = \frac{3 c^{3}}{32 π^{2} h ν^{3}} .$

154. By the determination of $p$ the question regarding the properties of the state of statistical equilibrium between the system of the oscillators and the vibration exciting them receives a general answer. For from (265) we get

$η = \frac{1}{1 + p I}$

and further from (262)

(269)

$R_{n} = \frac{1}{ε} \frac{{(p I)}^{n}}{{(1 + p I)}^{n + 1}} .$

Hence in the state of stationary equilibrium the number of oscillators whose energy lies between $n h ν$ and $(n + 1) h ν$ is, from equation (253),

(270)

$N \int_{0}^{ε} R_{n} d ρ = N R_{n} ε = N \frac{{(p I)}^{n}}{{(1 + p I)}^{n + 1}}$

where $n = 0$ , $1$ , $2$ , $3, \dots$ .

Chapter III

51H. Hertz, Wied. Ann. 36, p. 12, 1889.